Simple question right?
This website, along with the Calc book we’re teaching from, define it this way:
A point where the graph of a function has a tangent line and where the concavity changes is a point of inflection.
There’s no debate about functions like , which has an unambiguous inflection point at
.
In fact, I think we’re all in agreement that:
- There has to be a change in concavity. That is, we require that for
we have
and for
we have
, or vice versa.*
- The original function
has to be continuous at
. That is,
does not have a point of inflection at
even though there’s a concavity change because
isn’t even defined here. If we then piecewise-define
so that it carries the same values except at
for which we define
, we still don’t consider this a point of inflection because of the lack of continuity.

The point of inflection x=0 is at a location without a first derivative. A “tangent line” still exists, however.
But the part of the definition that requires to have a tangent line is problematic, in my opinion. I know why they say it this way, of course. They want to capture functions that have a concavity change across a vertical tangent line, such as
. Here we have a concavity change (concave up to concave down) across
and there is a tangent line (
) but
is undefined.
So It’s clear that this definition is built to include vertical tangents. It’s also obvious that the definition is built in such a way as to exclude cusps and corners. Why? What’s wrong with a cusp or corner being a point of inflection? I would claim that the piecewise-defined function shown above has a point of inflection at
even though no tangent line exists here.
I prefer the definition:
A point where the graph of a function is continuous and where the concavity changes is a point of inflection.
That is, I would only require the two conditions listed at the beginning of this post. What do you think?
Once you’re done thinking about that, consider this strange example that has no point of inflection even though there’s a concavity change. As my colleague Matt suggests, could we consider this a region of inflection? Now we’re just being silly, right?
———————————————
Footnotes:
* When we say that a function is concave up or down on a certain interval, we actually mean or
for the whole interval except at finitely many locations. If there are point discontinuities, we still consider the interval to have the same concavity.
** This source, interestingly, seems to require differentiability at the point. I think most of us would agree this is too strong a requirement, right?




I think x^(2/3) has a vertical tangent line at x=0, even though x=0 is a cusp point. How is it different from x^(1/3) in that respect?
I think that a definition can be anything someone wants. So the real questions are: (1) What’s the most popular (straight count of textbooks, or Wikipedia, Wolfram Alpha, etc.)? And, (2) what is the purpose for giving a name to the thing that we’re talking about? We don’t have a special name for a place where the slope of a tangent is 1.
hmm.. you’re right that x^(2/3) has a tangent line. Can we think of another function, then, perhaps piecewise-defined, like f(x)=x^(1/3) for x>=0 and f(x)=x^2 for x<0 which is continuous at x=0, changes concavity, but doesn't have a tangent line? What would prevent this from being an inflection point in anyone's mind?
I'll have to update my post!
From three days i am in this problem…….. finally solved.that we have to change the definition or exclude the one condition from the definition
The difference is that for x^(1/3), there IS a change in concavity at x = 0. For x^(2/3), there is NOT a change in concavity at x = 0. The fact that there is a tangent line to x^(2/3) at x = 0 is immaterial because for that function, there is NOT change in concavity at x = 0, ergo NO inflection point there.
Yes, a bad example for TWO reasons :-).
The main ambiguity mentioned in my post still stands!
Backing off to extrema and first derivative, we know that not all places with 0 deriv. are extrema and not all extrema are at places where deriv. are 0 (since there are endpoints, cusps, jump discontinuities). Furthermore, there are an infinite number of minima for the function f(x)=5 with domain all Reals; they happen to be at every point of the domain; also the same points are all maxima. (I am assuming that the definition of max at x means a point (a, f(a)) for which f(a)
>= f(x) for all x in some neighborhood of a. Notice weak inequality, >=, not strong inequality, >.)
Now an analogy. Rising, falling, max, and min are to first derivatives as concave up, concave down, and inflexion [British spelling is one less letter to type] are to second derivatives. So to be consistent with what I said in the first paragraph, not all inflexion points are places where the second deriv. is 0. They can be at pts where deriv. is undefined. Just as a max separates rising from falling, so an inflexion pt separates concave down from concave up. So I have no problem with Matt’s “region of inflexion.”
I find it helpful to remember that we bring a coordinate system to a problem, not the other way around, so the curve y^3 = x^2 and the curve x^3 = y^2 are the same curve, which just happen to be expressed in different coordinate systems. (Reflected along the line y=x.) In one case we don’t even have a function, but that’s just an accident of the coordinate system. I think that an inflection point is an intrinsic property of a curve, and so being concerned about whether a tangent is vertical is a red herring. One can make the tangent non-vertical just by changing the coordinate system, without changing the curve. Think of a curve as parametrized by arc length, for example.
Now I’m prepared to answer my own question. We don’t have a separate name for a point on a curve where the tangent’s slope is 1 because that’s not an intrinsic part of the curve. We do have a name for an inflexion pt because it can be described by intrinsic geometry, using curvature. An inflexion pt is where the curvature changes sign.
Do you hear the inflection in my voice?
Hi dad!
I’ve never liked thinking of ‘every point’ on the graph of y=5 being a max or min, but I’ve seen the definition enough to accept it when it’s used. So I think I’m fine with a whole ‘region of inflection.’ But by the same logic, this would also force us into saying that a graph like y=5 is concave up AND concave down everywhere. Right? (just like it’s increasing AND decreasing everywhere). I’m not sure if I agree with that, though.
On the second point, I have no problem with vertical vs. horizontal tangent lines. I don’t think anyone disputes the fact that![y=\sqrt[3]{x}](https://s0.wp.com/latex.php?latex=y%3D%5Csqrt%5B3%5D%7Bx%7D&bg=ffffff&fg=333333&s=0&c=20201002) has an inflection point at
has an inflection point at 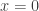 . I have a problem with requiring that an inflection point ‘have a tangent line.’ It feels like my green piecewise-defined function should have an inflection point at
. I have a problem with requiring that an inflection point ‘have a tangent line.’ It feels like my green piecewise-defined function should have an inflection point at 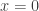 but by our Calculus book definition, it doesn’t.
but by our Calculus book definition, it doesn’t.
Nice post! I like that “region of inflection” example.
I guess the choice of “continuious at the point” or “having a tangent line at the point” depends, like your dad says, on what points of inflection are for. He’s right that it makes sense to think of them as properties of a curve’s geometry, in which case maybe we want to exclude cusp points. (A point of inflection, in this view, is a special type of differentiable point.)
But I tend to like your “continuous” definition better. The second derivative has a very clear physical interpretation (as acceleration). I like thinking of a point of inflection not as a geometric feature of the graph, but as a moment when the acceleration changes. And for that, we don’t need smoothness, just continuity.
Anyway, fun definitional question.
I’m also with you on the strangeness of having every point on a constant function’s graph qualify as both a max and a min. (I used to define max and min for my students using strict equality, before realizing it was totally nonstandard.) Luckily, I don’t think the argument extends to calling a constant function “increasing” or “decreasing” (since its derivative is decidedly zero).
Thanks for stopping by, Ben! And thanks for your great comments, too.
I think many *would* in fact treat a constant function as “increasing” (and decreasing) since it satisfies for
for 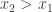 . That being said, a constant function *wouldn’t* be considered ‘strictly increasing.’
. That being said, a constant function *wouldn’t* be considered ‘strictly increasing.’
I’m not sure I like this looser definition of increasing, but you’re right, it is somewhat standard.
Hmmm… you’re right. I’ve been defining “strictly increasing” for my students and just calling it “increasing.”
consisting of two pieces which meet at x=4. This function must contain the following four points:
(0,2), (3,5), (5,-1), (8,2)
We were looking to find a piecewise quadratic function consisting of two pieces which meet at x=4. This function must contain the following four points:
(0,2), (3,5), (5,-1), (8,2)
that was continuous and differentiable.
We came up with
f(x) =
-x^2 + 4x +2 for 0 < x < 4
2 for x = 4
x^2 – 12 x + 34 for 4<x<=8
We feel like it clearly has both a tangent line at (4, 2) as well as a point of inflection at (4, 2) even though the second derivative doesn't exist
What a great example, Dennis!
We’ve seen some examples where we have a POI, and BOTH the first and second derivative fail to exist. (Like![y=\sqrt[3]{x}](https://s0.wp.com/latex.php?latex=y%3D%5Csqrt%5B3%5D%7Bx%7D&bg=ffffff&fg=333333&s=0&c=20201002) or
or  or my green piecewise function.)
or my green piecewise function.)
I think it’s nice to see an example, though, where we clearly have a POI but the first derivative DOES exist and the second derivative DOES NOT.
Another example would be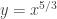 .
.
Cool!
I think the larger problem is that there is no simple intuitive rigorous definition of what a tangent line is. Give me your definition and I will shoot it down with counterexamples.
This is an interesting point, Will. I want to think about it some more.
But I’m not sure you’ve highlighted the “larger problem” when it comes to POI, unless you demand that there be a tangent line at a POI. Do you? I don’t, so I discard immediately any discussion of tangent lines.
Well, if your definition of the tangent line to at
at  is just a line through
is just a line through  with slope equal to
with slope equal to 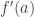 , then
, then ![f(x) = \sqrt[3]{x}](https://s0.wp.com/latex.php?latex=f%28x%29+%3D+%5Csqrt%5B3%5D%7Bx%7D&bg=ffffff&fg=333333&s=0&c=20201002) would not have a tangent at
would not have a tangent at 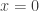 .
.
I don’t require there to be a tangent line in order for there to be a POI.
Let me try to answer this a different way. Is a point of inflection an intuitively clear idea? Is there a natural class of objects that we all recognize as points of inflection that we merely need to take care to define rigorously?
I suspect that if you asked someone 200 years ago what a relative maximum was, you’d get something like this: A relative maximum is a point where a function stops increasing and starts decreasing. But in our attempts to define a relative maximum precisely (and in our relatively liberal attitude to what counts as a function), we are forced to accept relative maxima such as when
when 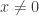 and
and 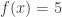 when
when 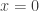 and the fact that constant functions have relative maxima everywhere.
and the fact that constant functions have relative maxima everywhere.
Similarly, perhaps we have an intuitive idea of what a point of inflection is: it’s a point where a function stops speeding up and starts slowing down or stops slowing down and starts speeding up.
If your primary goal is to characterize these points for what they say about what is happening to the rate at which the function is changing, then you could see why you might insist that, for example,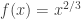 doesn’t have a point of inflection at
doesn’t have a point of inflection at 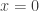 .
.
If, on the other hand, you’re simply interested in keeping track of where the concavity changes, then I don’t see why you’d even insist on continuity. After all, as the above example shows, we don’t insist on continuity to classify a point as a relative maximum.
I only suggest continuity as a requirement because it seems ill-defined to talk about a “point” of inflection if there really isn’t a well-defined point on the curve. The most important thing is a concavity change, obviously. Beyond that, I think the requirements should be pretty loose. I think continuity is a fair requirement. For example, I don’t want to say that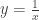 has a “point” of inflection at
has a “point” of inflection at 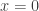 .
.
What requirement would you choose, Will?
But if we define when
when 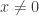 and
and 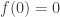 when
when 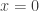 , now f is defined at
, now f is defined at 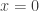 . Is
. Is 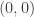 a point of inflection?
a point of inflection?
I don’t really have a solution that I find totally satisfactory.
Yeah,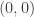 doesn’t feel like a point of inflection for the informal reason that the concavity doesn’t change “at that particular location.” It changes …like…at infinity or something. That’s why I said continuity seems like a reasonable requirement that we can all agree on, at least. We might even be able to be looser, but I’m not sure we’ll get agreement on any looser definition.
doesn’t feel like a point of inflection for the informal reason that the concavity doesn’t change “at that particular location.” It changes …like…at infinity or something. That’s why I said continuity seems like a reasonable requirement that we can all agree on, at least. We might even be able to be looser, but I’m not sure we’ll get agreement on any looser definition.
Do you agree, at least, that there’s no need to require a tangent line at a POI?
This has also been bugging me for a while now. I just e-mailed Wolfram, asking if it is really necessary for the second derivative to be 0 at an inflection point as they state in their website. Do you teach AP? I’m wondering what’s the stance of College Board regarding this.
I think that when AP asks a student to consider if x=a is a point of inflection, they will ensure that the function under consideration is continuous at x=a. That is, they will just try to avoid the issue altogether, ONLY considering points of inflection that are points of inflection under virtually ALL reasonable definitions. “Avoid the issue” is my call on this one.
They avoid the issue on many other things too. For example (this is just the first thing I thought of…I’m sure there are others), they will never ask students to evaluate the indefinite integral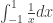 (some say this diverges, some say this is 0–the Cauchy Principal Value of the integral) but they WILL have students evaluate the indefinite integral
(some say this diverges, some say this is 0–the Cauchy Principal Value of the integral) but they WILL have students evaluate the indefinite integral  because by all accounts, this diverges. They just want to avoid the nuance of this conversation entirely, which I completely understand.
because by all accounts, this diverges. They just want to avoid the nuance of this conversation entirely, which I completely understand.
I have always considered the “shark fin” function to have point of inflection at x=0 (this is the function y=x^2 for x<0 and y=x^(1/3) for x≥0. So I am of the camp where a point of inflection is a place on a curve where the function is continuous there, and the concavity is changing sign.
I had the exact same doubt.I don’t get why is a tangent necessary for a point of inflection.The presence of tangent at that point doesn’t make any difference to the change in concavity which I think is the most important condition.If we follow the more accepted definition (Although I didn’t find any other exchanges regarding this problem, which is surprising) x=0 (In the function you described) will not be a point of inflection solely because it doesn’t have a tangent.So if a function doesn’t have a second derivative at a point then it must have a vertical tangent and satisfy the obvious conditions to be called a point of inflection.I hope it helps(But if you wanted to know the reason then I don’t know that)